
| Monday, June 23 | Tuesday, June 24 | Wednesday, June 25 | |
|---|---|---|---|
| Keynote talks | 8:30 - 9:30 | 8:30 - 9:30 | 8:30 - 9:30 |
| Break | 9:30 - 10:00 | 9:30 - 10:00 | 9:30 - 10:00 |
| Invited talks | 10:00 - 11:40 | 10:00 - 11:40 | 10:00 - 11:40 |
| Lunch | 11:40 - 13:30 | 11:40 - 13:30 | 11:40 - 13:30 |
| Invited/Contributed talks | 13:30 - 15:10 | 13:30 - 15:10 | 13:30 - 15:10 |
| Break | 15:10 - 15:40 | 15:10 - 15:40 | 15:10 - 15:40 |
| Invited/Contributed talks | 15:40 - 17:20 | 15:40 - 17:20 | 15:40 - 17:20 |
All talk sessions are held in Room 1700, 1315, 1325, 1520
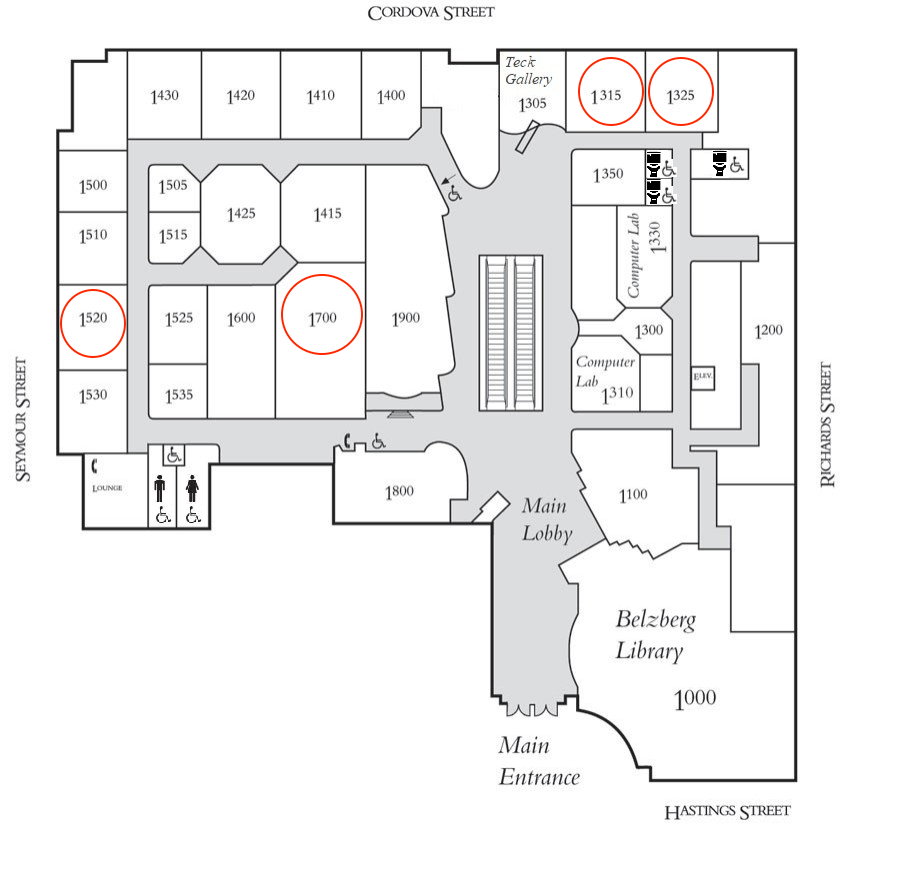 Map of Harbour Center SFU 1st Floor
Map of Harbour Center SFU 1st Floor
Monday, June 23 8:30-9:30 HC1700 Labatt Hall
Speaker: Jane-Ling Wang, University of California Davis
Chair: Nancy Heckman, University of British Columbia
Title: Hypothesis testing for black-box survival models
Abstract: Deep learning has become enormously popular in the analysis of complex data, including event time
measurements with censoring. To date, deep survival methods have mainly focused on prediction. Such methods are
scarcely used in statistical inference such as hypothesis testing. Due to their black-box nature, deep-learned
outcomes lack interpretability which limits their use for decision-making in biomedical applications. Moreover,
conventional tests fail to produce reliable type I errors due to the ability of deep neural networks to learn
the
data structure under the null hypothesis even if they search over the full space. This talk provides testing
methods
for survival models and demonstrates its use in the nonparametric Cox model, where the nonparametric link
function
is modeled via a deep neural network. To perform hypothesis testing, we utilize sample splitting and
cross-fitting
procedures to get neural network estimators and construct the test statistic. These procedures enable us to
propose
a new significance test to examine the association of certain covariates with event times. We show that the test
statistic converges to a normal distribution under the null hypothesis and establish its consistency, in terms
of
the Type II error, under the alternative hypothesis. Numerical simulations and a real data application
demonstrate
the usefulness of the proposed test.
Tuesday, June 24 8:30-9:30 HC1700 Labatt Hall
Speaker: Hans-Georg Müller, University of California Davis
Chair: Liangliang Wang, Simon Fraser University
Title: Uncertainty Quantification for Random Objects Through Conformal Inference
Abstract: Quantifying the centrality for object-valued responses, i.e., data situated in general metric spaces
such as compositional data, networks, distributions, covariance matrices and also high-dimensional and
functional data paired with Euclidean predictors, is of interest for many statistical applications. We employ a
conformal approach that utilizes conditional optimal transport costs for distance profiles, which correspond to
one-dimensional distributions of probability mass falling into balls of increasing radius. The average transport
cost to transport a given distance profile to all other distance profiles is the basis for the proposed
conditional profile scores and the distribution of these costs leads to the proposed conformity score. Uniform
convergence of this conformity score estimators imply the asymptotic conditional validity for the resulting
prediction sets, which quantify the uncertainty inherent in a new observation. The proposed conditional profile
score can be used to determine the outlyingness of a new observation as we demonstrate for various data,
including longitudinal compositional data reflecting brain development of children. This talk is based on joint
work with Hang Zhou and Yidong Zhou.
Wednesday, June 25 8:30-9:30 HC1700 Labatt Hall
Speaker: Martin Ester, Simon Fraser University
Chair: Ke Li, Simon Fraser University
Title: A machine learning approach for causal inference from observational data
Abstract: Causal inference, i.e. the estimation of treatment effects from observational data, has many applications in domains such as public health, personalized medicine, economics, and recommender systems. Different from randomized controlled trials, in observational data treatment assignment is not random, but depends in an unknown way on some confounder(s). This selection bias poses a major challenge for causal inference, since outcomes recorded in the dataset measure the combined effect of the treatment and the confounder. In the machine learning community, the representation learning approach has demonstrated remarkable success in adjusting for the covariate shift induced by selection bias. The idea is to learn a balanced representation of covariates, i.e. a latent representation that has a similar distribution for the treatment and control groups, rather than balancing the covariates themselves. In this talk, we will introduce the machine learning approach and discuss methods for various scenarios, including Boolean treatments, continuous treatments, and multiple treatments. We will conclude with a discussion of future research directions.